Introduction

In Part 1 of this series, we had a look at quite a lot of concepts! We saw how to get started with Ceylon and its IDE, what types (String, Boolean etc) and values ("Hello", true) are, functions (function add(Float x, Float y) => x + y), lists (Sequences and Tuples: [1, 2, 3], Iterables: {'a', 'b', 'c'}), loops (for and while), conditionals (if then else), comprehensions ({ for (a in as) a.something }), and finally, variadic parameters (function takeManyStrings(String* strings) => ...).

We also created a first, more or less complete program, the Maths Helper, that allows users to do some simple maths.

In this part of the series, we will start looking at some more advanced concepts, such as union types, switches, custom types, enumerated types, polymorphism, generics and finally, mutability and data structures.

Ceylon discourages the use of mutability. By default, everything in Ceylon is immutable. We will discuss why that is in the last section of this tutorial.

These concepts will allow you to tackle problems with a high level of complexity in a manageable manner.

To get started, let’s have a look at one of the most innovative features of Ceylon: union types.

Union types

You might remember the askUserForNumber function, from Part 1, which asked the user for a Number and returned either the number the user entered or null, ie. no value, if the user did not enter a valid number:

Float? askUserForNumber(String question) { ... }

We already mentioned then that Float? is just short notation for the type Float | Null, which reads as Float or Null.

This is called a union type.

A union type is a type formed by two or more different types. A value always has a single type, but a function may accept or return values of different types. That’s the main reason union types exist.

To try this out, you can use the following code (don’t forget, this must be inside the run function):

Float? askUserForNumber(String question) {
	process.write(question);
	value userX = process.readLine();
	return parseFloat(userX);
}

value x = askUserForNumber("Enter a number (x): ");
print(x exists then "Thank you!" else "Sorry, that's not a number.");

We show above how you can use then … else directly in a single expression… you just need something that evaluates to a Boolean before then, and an expression that evaluates to some value in case that’s true and another in case that’s false.

Any number of types can be part of a union. Here are some examples:

void show(String|Boolean|Integer input) {
    String type;
    if (is String input) {
        type = "String";
    } else if (is Boolean input) {
        type = "Boolean";
    } else {
        type = "Integer";
    }
    print("``type``: ``input``");
}

show("hello"); // prints 'String: hello'
show(true);    // prints 'Boolean: true'
show(400);     // prints 'Integer: 400'

// convert a String into an Integer, Float or Boolean, whatever possible,
// or just return the String itself if none was possible.
Integer|Float|Boolean|String convert(String string) {
    return parseInteger(string) 
    else parseFloat(string)
    else parseBoolean(string)
    else string;
}

assert(convert("true") is Boolean);
assert(convert("1") is Integer);
assert(convert("1.0") is Float);
assert(convert("Just String") is String);

These examples are a little bit artificial but should already show the possibilities union types bring to the table. To truly understand how union types can be extremely useful, however, we must first learn how to define our own types.

A particularly useful construct to deal with union types is the switch, which we will meet soon.

Defining our own types

All types we have talked about so far (String, Boolean, Float, Integer, Character) are defined by Ceylon itself and available to any Ceylon program. We can achieve a lot using only these types, but to model the real world, it is very convenient to be able to define our own types so that it becomes more natural to reason about the problems we are trying to solve.

In Ceylon, there are four different ways one can define a type:

• alias
• class
• interface
• abstract class

The easiest way to define a type is to just borrow an existing definition and call it our own! That’s what alias does.

Alias

Sometimes, we want to declare a type which is very simple, or similar to another existing type, but we still believe it would be useful to create that type to make code easier to understand.

A common use-case for this is to keep people’s names. A String might seem adequate enough for a simple name, but that would allow empty names to exist. So we may want to use [Character+] instead. And perhaps a sequence of [Character+] for the full name. The problem is that we would end up with types like this:

// parse a name, returning either a full name or null if the given input was empty
[[Character+]+]? parseName(String input) { ... }

But we can make code like this much more readable by defining some aliases, as in this example:

alias Name => [Character+];
alias FullName => [Name+];

// parse a name, returning either a full name or null if the given input was empty
FullName? parseName(String input) {
    function stringAsSequence(String s) => s.trimmed.sequence;
    value parts = [ for (part in input.split().map(stringAsSequence))
                    if (nonempty part) part ];
    if (nonempty parts) {
        return parts;
    } else {
        return null;
    }
}

FullName? myName = parseName("Renato Athaydes");
assert(is FullName myName, myName == ["Renato", "Athaydes"]);

FullName? noname = parseName("");
assert(noname is Null);

FullName? emptyName = parseName("    ");
assert(emptyName is Null);

Aliases can also be useful to make large union types nicer on the eye. For example, we could improve the declaration of convert in the previous section by defining an alias for Integer|Float|Boolean|String:

alias Convertable => Integer|Float|Boolean|String;

Convertable convert(String string) {
    return parseInteger(string) 
    else parseFloat(string)
    else parseBoolean(string)
    else string;
}

This is especially useful when such kind of type appears in a lot of places, so you don’t need to re-write (or read) the large type name again and again.

Aliases do not actually create new types, they simply ‘rename’ an existing type or a simple type expression.

Besides type aliases, Ceylon also has class aliases which can be used to give an existing class a different name:

class NameList({FullName?*} name) => Array<FullName?>(name);

Class aliases, unlike type aliases, can be used to create instances of the aliased type, as the example below demonstrates:

"Creates a valid FullName, or null if not possible"
FullName? name(String fullName) {
    value nameParts = [ for (part in fullName.split()) 
                        if (nonempty n = part.sequence) n ];
    if (nonempty nameParts) {
        return nameParts;
    } else {
        return null;
    }
}

value names = NameList({ "John Smith", "Anna Brown", "" }.map(name));

// print the first names
for (fullName in names) {
    print("First Name: ``fullName?.first else "<INVALID>"``");
}

In the expression fullName?.first, the question mark enables “null-safe” property access. It allows us to get the value of the property first of fullName if fullName is not null, and if it is null, the whole expression evaluates to null.

Running this prints:

First Name: John
First Name: Anna
First Name: <INVALID>

Custom types with classes

Imagine we want to model playing cards to create a cards game. With what we know so far, we would have to improvise and use types like String and Integer, or some aliases, to represent the cards. That might actually work, but there’s a much nicer way to model things in Ceylon: to create a class for the object you want to model.

A simple class declaration may look like the following:

class Card(shared Integer rank, shared Integer suit) {}

value card = Card(5, 3);
assert(card.rank == 5);
assert(card.suit == 3);

The above declaration defines a class called Card which contains the fields rank and suit. Because the fields are shared, they can be accessed as properties of a card instance.

Using Integer as the type of both rank and suit seems misguided. What would the Integer corresponding to hearts, or Queen, be? We can do much better than that by defining more new types for these as well:

// suites
class Spades() {}
class Diamonds() {}
class Hearts() {}
class Clubs() {}

// ranks
class Ace() {}
class Jack() {}
class Queen() {}
class King() {}

alias Rank => Integer|Ace|Jack|Queen|King;
alias Suit => Spades|Diamonds|Hearts|Clubs;

// definition of a playing card
class Card(shared Rank rank, shared Suit suit) {}

// example of a card
Card aceOfSpades = Card(Ace(), Spades());

This is looking good, but there’s a problem with our definition of Rank: it still allows any Integer to be a valid rank, but as we know, in any game of cards, the rank is limited to just a few numbers, besides Ace, Jack, Queen and King.

The first solution that might come to mind might be to modify the Card class declaration to check that the value provided for the rank is valid in case it is an Integer (in the other cases, no check is needed, of course):

class Card(shared Rank rank, shared Suit suit) {
    if (is Integer rank) {
        assert(rank in 2..10);
    }
}

That is a valid solution, it makes it impossible for anyone to instantiate an invalid card. But it makes it possible to try to instantiate an invalid card, which would result in an Error!

// this will throw an Error
value invalidCard = Card(300, Hearts());
print("Will never get here");

An arguably better solution would be to enumerate each valid value, just like we did for Suit:

// ranks
class Ace() {}
class Two() {}
class Three() {}
class Four() {}
class Five() {}
class Six() {}
class Seven() {}
class Jack() {}
class Queen() {}
class King() {}

alias Rank => Ace|Two|Three|Four|Five|Six|Seven|Jack|Queen|King;

Now it is just impossible to even try to instantiate an invalid card! The problem is that enumerating all values might not be always possible. In that case, the previous solution might be the only viable alternative. But keep in mind that every time you run into this problem, you should try to minimize the possibility of a run-time error being possible, as that can quickly become un-manageable and is the source of countless bugs in real software.

Interfaces

Quite often, we come across concepts which have the same kind of properties, but differ only in the details of how they behave. Continuing with our game, we may think of one example of this as being a dealer. Whatever the game we decide to create may be, we will probably need a dealer. There are many things a dealer can do, and most of them do not depend on which game is being played, such as dealing the cards, shuffling and perhaps comparing players’ hands.

This is a good example of where we could use an interface to model a fairly abstract concept.

An interface is an abstract definition of a particular concept which we want to model. In other words, it can be seen as a contract which may be satisfied by concrete or abstract classes to provide the actual behavior.

Before we define our first interface, we must formally define what a method is:

A method is simply a shared function that is declared inside a class or interface. It is useful to make that distinction because methods can have access to internals of a class which are not available to other functions, so methods, unlike functions, can be seen as being an integral part of the class or interface in which they are defined.

Ok, now that we know the theory, let’s give that a go:

// first, some definitions
alias Hand => {Card*};
alias Pack => {Card+};

interface Dealer {    
    shared formal Pack shuffle(Pack pack);
    
    shared formal Hand dealHand(Pack cards);
    
    shared formal Comparison compareHands(Hand hand1, Hand hand2);
    
    shared default {Hand+} deal(Pack cards, Integer playersCount) =>
        (1..playersCount).map((Integer i) => dealHand(cards));
        
}

Notice that each method of an interface which does not have a default implementation must be declared formal. Default implementations can be provided and might be declared default (if not marked default, the method cannot be refined by implementations of the interface).

Dealer is just a concept, it does not define how to do anything (notice how the formal methods have no body) except for the trivial case of defining the deal method, as that can be easily done in terms of the formal method dealHand, even if we do not yet have a concrete implementation of that method. The actual behavior of a Dealer must be provided by implementation classes.

This is very useful as it allows us to write other parts of the game which do not depend upon the specific rules of our game before we even know what our game rules are going to look like. And notice that there could even be more than one game (and therefore different implementations of Dealer), but the parts of the game which will not be impacted by the specifics of each game can still be written only once.

Notice that, because interfaces do not implement all the behavior that would be necessary to actually use an instance of it, you cannot instantiate an interface directly!

The following results in a compiler error (so you can’t even run this program):

// does not compile!
value dealer = Dealer();

// what would this return if this compiled?
value hand = dealer.dealHand(pack);

For this reason, before we can instantiate a subtype of Dealer, we will have to provide at least one implementation for it.

To implement an interface is very simple. You must provide an implementation for each formal method. Here’s a “dummy” implementation of the Dealer interface defined above:

class DummyDealer() satisfies Dealer {
    
    shared actual Pack shuffle(Pack pack) => pack;
    
    shared actual Hand dealHand(Pack cards) => { Card(Ace(), Hearts()) };

    shared actual Comparison compareHands(Hand hand1, Hand hand2) => larger;
    
}

This kind of “dummy” implementation (it is called dummy because it does not really implement the behavior, notice how shuffle does not really shuffle the pack, and dealHand just returns the same hand every time) is useful for developing large systems gradually so you don’t need to implement the whole system before you can even run anything.

Ceylon has a nice short notation for writing actual methods with a single expression (using =>): you can just omit everything before the name of the method, so the above definition could be written more concisely as:

class DummyDealer() satisfies Dealer {
    
    shuffle(Pack pack) => pack;
    
    dealHand(Pack cards) => { Card(Ace(), Hearts()) };

    compareHands(Hand hand1, Hand hand2) => larger;
    
}

Although Ceylon aims at making code readable and mostly explicit, it makes an exception in the case of overriding formal methods or properties because this is such a common case and no information is lost - if you ever see a method that does not seem declare its return type, you know it’s because you’re seeing this notation and the return type is already declared in the interface.

But beware that if you use this notation, it will be implied that the method is declared shared actual. If you want to make your method definition default, which means that you want to allow sub-classes to refine the method definition if desired, you would need to explicitly declare it with shared actual default followed by the full type signature.

See the Ceylon Language Specification’s chapter on interfaces for the full story.

Syntax-sugar for operators by implementing interfaces

Ceylon provides some syntax sugar to make code more readable through the use of certain interfaces.

For example, in Part 1, we saw how the Integer’s methods plus, minus, divided, times and remainder are equivalent to using the operators +, -, /, * and % respectively.

So, instead of writing 2.plus(2) == 4 we can write 2 + 2 == 4.

The only reason why that is possible is because Integer satisfies the interfaces Summable (which defines plus, or +), Numeric (which defines minus, divided and times, or -, / and *) and Integral (which defines remainder, or %).

Summable is a generic type, which means that it always appears in the form Summable<Element>, where Element is a type parameter - it can be replaced with any type… or at least some allowed types, as we will see later when we discuss generics.

Anyone could write a type that satisfies Summable, to pick one of the interfaces mentioned above, to be able to use the + operator to add together two instances of that type.

As an example, we can make a Summable kind of Iterable so that we can add two Iterables together:

Notice that in Ceylon, normally, you cannot add two Iterables with the + operator. The reason why Ceylon seemingly lacks this functionality is that implementing plus for a generic Iterable would likely break the contract of Summable that requires that the + operation be associative. For example, { 1, 2 } + { 3 } would have to be the same as { 3 } + { 1, 2 }. In the definition of SummableList below, we get around that fact by adding the constraints that SummableList contains only Integers and is always sorted, so that SummableList { 1, 2 } + SummableList { 3 } == SummableList { 3 } + SummableList { 1, 2 }.

// necessary renaming to avoid clash with Iterable.sort in SummableList
import ceylon.language { doSort = sort }

"An always sorted Iterable containing Integers that can be summed."
class SummableList({Integer*} integers)
    satisfies Summable<SummableList> & Iterable<Integer> {
    
    {Integer*} _integers = doSort(integers);
    
    shared actual SummableList plus(SummableList other) =>
            SummableList(this._integers.chain(other._integers));
    
    shared actual Iterator<Integer> iterator() => _integers.iterator();
    
}

SummableList list1 = SummableList { 1, 2 } + SummableList { 3 };
SummableList list2 = SummableList { 3 } + SummableList { 1, 2 };
assert(list1.sequence == [1, 2, 3]);
assert(list2.sequence == [1, 2, 3]);

The example above, incidentally, shows how a class can declare that it satisfies more than one interface.

A class may declare that it satisfies more than one interface by using the & symbol between each interface name. What this symbol does is similar to what | does for union types, but results in an intersection type. Whereas an instance of a union type A|B can be either an instance of A or of B, an instance of A&B is an instance of both A and B. That is why, in the example above, an instance of SummableList, which satisfies types Summable<SummableList> and Iterable<Integer>, can be assigned to either type.

It also shows how you can import an element and rename it to avoid name clashes (if we didn’t rename sort to doSort, it would have clashed with Iterable’s own sort method inside the definition of SummableList, causing a compiling error because we are not allowed to use an inherited member in the class initializer).

One important thing to notice is that when a type satisfies an interface, besides being forced to implement all formal methods and properties, it inherits all of its default methods.

For this reason, SummableList gets a large number of methods pretty much for free:

value myList = SummableList { 30, 20, 10 };
assert(myList.size == 3);
assert(exists first = myList.first, first == 10);
assert(exists last = myList.last, last == 30);
assert(exists item = myList.find((Integer elem) => elem > 10), item == 20);
assert(myList.takingWhile((Integer elem) => elem < 15).sequence == [10]);
assert(20 in myList);

The in operator maps to method contains of Iterable, so because SummableList satisfies Iterable, we can use the in operator to test if a SummableList contains a certain element, as shown in the last example above.

If we wanted to make it possible to compare instances of SummableList with the comparison operators (<, <=, >, >=, <=>), we would have to implement the Comparable interface, which requires only a single method: compare.

If we try to compare two instances of SummableList, we will notice that the results will not be as expected:

// this assertion fails
assert(SummableList { 1, 2 } == SummableList { 1, 2 });

That’s because of the way the == operator works. It maps to the equals method of the Object abstract class.

We will revisit the == operator (and also ===, which compares identity) once we learn more about abstract classes, objects and enumerated types.

Abstract classes

Finally, the last way in which we can create a type in Ceylon is by declaring an abstract class.

An abstract class is similar to an interface, but besides having formal and default methods and properties, it can also have a parameter list and hold state, like concrete classes. Unlike concrete classes, but like interfaces, abstract classes may not be instantiated.

A concrete class (ie. a non-abstract class) may only extend one abstract class. This restriction does not apply to interfaces. For this reason, it is usually preferable to use interfaces to define things unless you must hold internal state, which you cannot do in an interface.

In this context, state means having one or more fields.

On the other hand, abstract classes can still be very useful when there is some common functionality that can be implemented appropriately for most expected implementations of a concept in the same manner. This may sound like something that is rare in practice, but it actually happens quite often.

For example, a card game itself is a good candidate for an abstract class because any game will always have a number of players, a dealer (which can be a player him/herself) and at least one card pack.

Let’s try to express all of that in code (with the earlier definitions unaltered), using the most appropriate level of abstraction for each element of the game:

interface Player {
    shared formal String name;
}

abstract class Game(Pack pack, Dealer dealer, Player+ players) {
    shared formal void start();
}

class MyGame(Pack pack, Dealer dealer, Player+ players)
    extends Game(pack, dealer, *players) {
    
    shared actual void start() {
        //TODO create the game
    }
}

class SimplePlayer(shared actual String name)
        satisfies Player {}

class MyGameDealer(shared actual String name) 
        extends DummyDealer()
        satisfies Player {}

shared void runGame() {
    value players = [ MyGameDealer("John"), SimplePlayer("Mark") ];
    value pack = { Card(Ace(), Spades()), Card(Ace(), Hearts()) /* ... */ };
    
    value game = MyGame(pack, players.first, *players);
    game.start();
}

Objects and Enumerated types

When we defined game cards previously, we declared a lot of classes which do not have any property, they simply exist to enumerate the possible values of a suit or a rank.

There is a better way to enumerate values like this in Ceylon using objects.

An object is an instance of an anonymous class. Anonymous classes and objects are analogous to anonymous functions and lambdas, which we met in Part 1, but unlike lambdas, objects can be declared anywhere.

The following example shows the creation of some objects in their simplest form:

object someObject {}

object anotherObject {}

value referenceToSomeObject = someObject;

// like all custom types, objects extends Basic by default
print(someObject == anotherObject); // prints false
print(someObject == referenceToSomeObject); // prints true

Objects are useful, mostly, to represent things that can only be one… things that simply exist, like 4 or a, that don’t make sense to be created more than once.

In other words, we use objects when we do not want to have several instances of this thing hanging around.

That’s the case, for example, with Suit and Rank, which we defined using classes earlier. Every time we write Hearts() or Four() we are creating a new instance of Hearts and Four, respectively. Besides the obvious waste of computer memory, this is not desirable because of the fact that Four() == Four(), as just one example, will return false! One can even say that’s a bug in our current implementation!

Armed with our knowledge about objects and interfaces, we can now refactor our definition of Rank to make use of them:

interface Suit {}
object spades satisfies Suit {}
object diamonds satisfies Suit {}
object hearts satisfies Suit {}
object clubs satisfies Suit {}

This is much better! Now, if you compare the objects, you get the expected answers:

print(spades == spades); // prints true

We can say that we have come a long way towards representing game cards in Ceylon in just the best possible way.

But…

You probably guessed, there’s still a couple of issues with our definition!

First of all, anyone could break our game by carelessly defining a new type of Suit:

"Non-existing Suit"
object golds satisfies Suit {}

This makes it clear that we did not really enumerate ALL possible Suits in our definition. This has some other implications we’ll see later with the switch statement.

The thing is that it would be really, really nice if we could ensure that there’s only 4 types of Suits, the 4 types that we defined: spades, diamonds, hearts and clubs. No golds!

The second issue we still have to fix is that if you print one of our objects, spades, as an example, you will get something similar to this:

helloCeylon.spades_@7265d075

That’s not cool. When you print something, you should show some helpful information to the user (or the programmer debugging the code later).

Can we fix these problems? Sure we can!

For the first problem, we can use the of keyword to let Ceylon know what instances of our type can exist. In other words, to enumerate the possible values of something.

For the printing issue, there’s a simple solution: overwrite the string property (which is defined in Object) for each of our objects.

That’s the secret of print: it knows how to print any Object because every Object has the string property.

Putting the two solutions together, we get this beautiful definition of a Suit:

interface Suit of spades | diamonds | hearts | clubs {}
object spades satisfies Suit { string => "spades"; }
object diamonds satisfies Suit { string => "diamonds"; }
object hearts satisfies Suit { string => "hearts"; }
object clubs satisfies Suit { string => "clubs"; }

The syntax string => "something"; is again the short notation for shared actual String => "something".

Because we enumerated the possible values of Suit, it is just impossible to define any other Suit elsewhere. You can’t even create a class to satisfy Suit. Ceylon won’t let you! Your class would have to be enumerated after of for it to be allowed.

Notice that this trick works for abstract classes and classes as well, not only interfaces and objects (but the enumerated type itself must be an abstract class or interface):

abstract class A() of B | C {}
class B() extends A() {}
class C() extends A() {}

By the way, the Boolean type itself is defined as an enumerated type:

shared abstract class Boolean() 
        of true | false {}

shared object true extends Boolean() {
    string => "true";
}

shared object false extends Boolean() {
    string => "false";
}

Even null is just the single enumerated value of the type Null.

The switch statement

Ceylon has one more important statement which we haven’t seen yet: the switch.

The switch statement allows you to select which branch to execute depending on which case is satisfied:

Boolean condition = 4 > 2;
switch(condition)
case(true) {
    print("Condition is true");
}
case (false) {
    print("Condition is false");
}

The cases of a switch must be exhaustive, so it is impossible to forget to cover some case (the compiler makes sure of that).

If it is not possible to enumerate all cases (because the type of the variable used in the switch has infinite values, for example), you can add an else clause:

switch("abc")
case("a") {
    print("Case a");
}
case ("b") {
    print("Case b");
}
else {
    print("dunno");
}

Switches are very clever and can always figure out if you have covered all possible cases. Two very common use-cases for switches are to narrow the type of a value and to find out which of the enumerated types a value might have:

void show(Integer|Float|Boolean|String item) {
    switch(item)
    case (is Integer) {
        // here item has type Integer
        print("Integer ``item + 0``");
    }
    case (is Float) {
        print("Float ``item``");
    }
    case (is Boolean) {
        print("Boolean ``item``");
    }
    case (is String) {
        print("String ``item``");
    }
}

String suitOf(Card card) {
    switch(card.suit)
    case (clubs) {
        return "Clubs";
    }
    case (hearts) {
        return "Hearts";
    }
    case (diamonds) {
        return "Diamonds";
    }
    case (spades) {
        return "Spades";
    }
    // no other case is possible, so you don't need a return here
}

Polymorphism

Polymorphism is one of the most powerful concepts in programming. You may read a formal definition of polymorphism on Wikipedia if you are interested, but in this tutorial we’ll concern ourselves only with the practical uses of polymorphism.

The idea is really simple: you should be able to manipulate different things in the same way if they can be seen as being conceptually the same, even if only in certain contexts.

In practice, this means one of two things in Ceylon: sub-typing and generics.

Sub-typing

We have already met sub-typing a few times. Every time we satisfy an interface A in a class B, B becomes a subtype of A. It works the same way when a class X extends class Y: X becomes a subtype of Y (and Y a super-type of X).

Most of the time, a subtype can be seen, and treated, in the exact same way as its super-type(s). This becomes obvious when you consider that a subtype inherits all the behavior of its super-type(s).

Let’s look at a concrete example. We mentioned earlier that all custom types, by default, extend Basic.

Effectively, writing class A() {} is equivalent to writing class A() extends Basic() {}.

You can open any type declaration in the IDE by hitting Ctrl+Shift+T and entering the name of a type. Have a look at the definitions of Basic and Object! With a type opened, hit Ctrl+T to see the type hierarchy.

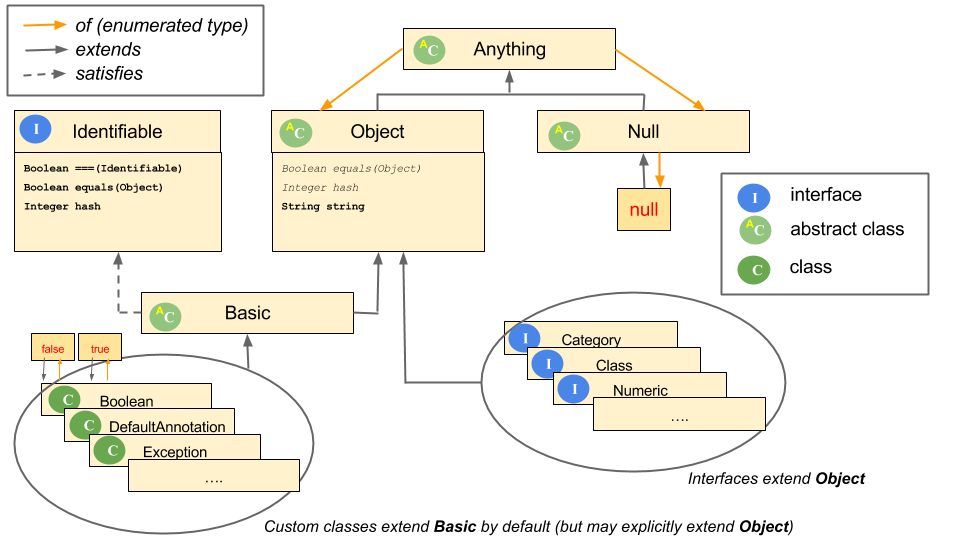The top part of the Ceylon type hierarchy

Basic does not define any property or method, but it extends Object and satisfies Identifiable.

Object has one formal method, equals, one formal property, hash, and provides a default implementation of string:

shared formal Boolean equals(Object that);

shared formal Integer hash;
    
shared default String string =>
        className(this) + "@" + hash.string;

The reason why custom types are not required to provide implementation for anything is that Identifiable, which is satisfied by Basic, provides default implementations for both equals and hash. This is really convenient, because equals, as we already saw, maps to the == operator, so that you can use the == operator with any custom type.

The === operator (notice it’s 3 =) is used to determine if two values are references to the same instance. It can be used with any type that satisfies Identifiable, and the default implementation of equals just delegates to ===:

shared default actual Boolean equals(Object that) {
    if (is Identifiable that) {
        return this === that;
    }
    else {
        return false;
    }
}

Now it should be obvious why we had an unexpected result when we tried to use the == operator to compare two instances of SummableList earlier on!

It is important to understand that just because you don’t need to implement equals, it doesn’t mean that you shouldn’t! In fact, you are encouraged to implement it for most types.

Just for completeness, let’s finally fix SummableList and make sure it respects the contract of Summable:

class SummableList({Integer*} integers)
    satisfies Summable<SummableList> & Iterable<Integer> {
    
    {Integer*} _integers = doSort(integers);
    
    plus(SummableList other) =>
        SummableList(this._integers.chain(other._integers));
    
    iterator() => _integers.iterator();
    
    hash => _integers.hash;
    
    shared actual Boolean equals(Object other) {
        if (is SummableList other) {
            return this.sequence == other.sequence;
        } else {
            return false;
        }
    }
    
}

Besides implementing equals, notice that we also implemented hash. That’s always a good idea because to respect the contract of Object, which states that if x == y then x.hash == y.hash, when you implement equals you must always implement hash as well. This is particularly important if your type may be added to a HashSet or a HashMap.

For a detailed explanation of the Ceylon type system, check the Ceylon Specification - Chapter 3.

Generics

You may not have known it, but you have already seen generic types before! In fact, all list types we saw before are generic, ie. they may contain items of any type (actually, the types may be bounded, as we’ll see).

Sequence<Integer> list1 = [1, 2, 3];
Iterable<String|Boolean> list2 = {"Hi", true, false, "Bye"};

Sequence<Integer> is a Sequence which can only hold Integers. Iterable<String|Boolean> is an Iterable which can only hold Strings or Booleans.

The type between the angle brackets (< >) is a type parameter for the generic type.

Before we explain this in more detail, let’s create a generic type to see how that’s done!

You might remember that earlier, we defined a type called SummableList that satisfied Iterable<Integer>… there’s no reason why this type should be usable only to hold Integers! As Iterable itself, we should allow it to hold values of any type.

Here’s a new definition of SummableList that fixes that problem using generics:

class SummableList<Element>({Element*} elements)
    satisfies Summable<SummableList<Element>> & Iterable<Element> {
    
    //FIXME these elements should be sorted! We must fix this later.
    {Element*} _elements = elements; // doSort(elements);
    
    plus(SummableList<Element> other) =>
        SummableList(this._elements.chain(other._elements));
    
    iterator() => _elements.iterator();
    
    hash => _elements.hash;
    
    shared actual Boolean equals(Object other) {
        if (is SummableList<Element> other) {
            return this.sequence == other.sequence;
        } else {
            return false;
        }
    }
    
}

The type Element above is not an actual type, it is only a type parameter which will be “replaced” with a concrete type when an actual instance of SummableList is created.

You can see in this code sample one of the techniques programmers often use during development: to add comments that start with FIXME to describe temporary solutions that need fixing later (but won’t affect the development of other parts of the system for some time) or TODO for things that need to be done, but cannot be done now for whatever reason. These are easily searchable (in the IDE, open Window > Show View > Tasks to see all your TODOs) so you can get back to them later. But not everyone likes that as it might encourage sloppy behavior if abused. It’s not uncommon to see hundreds of TODOs on large code bases that will probably go unnoticed for years, if not forever. You are warned, this can be useful, but use with care!

We can then use our new SummableList type as follows:

// normally, the type parameter is inferred
value stringList1 = SummableList { "ABC", "XYZ" };
value integerList1 = SummableList { 1, 2, 3 };

// but you can tell Ceylon what type it should be!
value stringList2 = SummableList<String> { "ABC", "XYZ" };
value integerList2 = SummableList<Integer> { 1, 2, 3 };

If you explicitly declare the type parameter as in the second example above, then all elements of the SummableList must be a subtype of that type.

Now, imagine if Iterable were not generic. It would be really painful to use! To access any element, it would be necessary to “narrow” its type (with if or assert) before trying to use it. And there would be no guarantee that the Iterable would not contain values of unexpected types, giving bugs a plentiful environment to prosper (this may all sound crazy, but in the dark days of computing - ie. 10 years ago or so - programming without generics was actually common-place and enabled by, among other sloppy techniques, type casting - or guessing the type - which Ceylon wisely does not even allow).

But there was a problem in the above implementation of SummableList (the one marked with FIXME). We no longer ensured that elements of the list were sorted. That was necessary for the current implementation of SummableList to compile for one simple reason: the sort function, that we use to sort the elements of the list, is a generic function!

That’s right, functions can also be generic! Take a look at the type signature of sort:

shared Element[] sort<Element>({Element*} elements) 
        given Element satisfies Comparable<Element> => ...

Ok, so it takes an Iterable of some type Element and returns a Sequential of the same type. So far so good, but you are probably wondering now what exactly is this given Element satisfies ... thing!

That’s actually really simple: given tells us (and Ceylon) that Element can be any type as long as (or given that) this type satisfies Comparable<Element>. We call this the “upper bound” of the type parameter. So in this case Comparable<Element> is the upper bound of the type parameter of the sort function.

When we say upper bound you can think back to the Ceylon type hierarchy diagram we showed earlier. Subtypes are generally shown below their supertypes. Giving a type parameter an upper bound is like saying that that type may not be “higher placed” in the hierarchy than some other type (the upper bound). Any types allowed by that upper bound are either exactly the same as the upper bound or subtypes of (below) it.

This is necessary for any sort function to work because to be able to sort a list, you must be able to compare an element to another… and any subtype of Comparable<Element> will have to implement the compare method, which guarantees to us that we can compare a value of this type with any other value of the same type!

Finally, we can address the FIXME in the previous implementation of SummableList. We could not use the sort function before because we did not restrict the type of the elements of SummableList, so there was no way to compare them to sort them. Now we can do exactly that and solve the problem:

import ceylon.language { doSort = sort }

class SummableList<Element>({Element*} elements)
        satisfies Summable<SummableList<Element>> & Iterable<Element>
        given Element satisfies Comparable<Element> {
    
    {Element*} _elements = doSort(elements);
    
    plus(SummableList<Element> other) =>
        SummableList(this._elements.chain(other._elements));
    
    iterator() => _elements.iterator();
    
    hash => _elements.hash;
    
    shared actual Boolean equals(Object other) {
        if (is SummableList<Element> other) {
            return this.sequence == other.sequence;
        } else {
            return false;
        }
    }
    
}

To make our types as re-usable as possible, we should try to restrict their type parameters with the most generic type (or highest bound) possible.

Making Element’s upper bound be Comparable<Element> is much better than, say, making it Scalar (which is a subtype of Comparable) because all functionality we require from our elements is provided by the higher bound, Comparable<Element>. Many programmers overlook this fact and needlessly restrict too much the types their functions and types can work with. The same is true also for arguments - they should always be of the most generic type for the code to do what it needs to do.

Often, you will have to make Object your type’s upper bound because if you do not do that, you will have to make sure your generic type or function also works with Null values.

Just like value parameters, there can be many type parameters and each one can be given a default value.

class TwoOrThreeThings<A, B, C = Null>(
    shared A a, shared B b, shared C c) {}

// the third type parameter defaults to Null
void printTwoThings(TwoOrThreeThings<String, Boolean> twoThings) {
    print("String is ``twoThings.a`` and Boolean is ``twoThings.b``");
}

// the third parameter is bound to Integer
void printThreeThings(TwoOrThreeThings<String, Boolean, Integer> threeThings) {
    print("* String is ``threeThings.a``
           * Boolean is ``threeThings.b``
           * Integer is ``threeThings.c``");
}

printTwoThings(TwoOrThreeThings("Hi", true, null));
printThreeThings(TwoOrThreeThings("Hi", true, 20));

Covariant and contravariant type parameters

Type parameters can be declared in 3 different ways:

• invariant: as all the type parameters we have met above.
• covariant: parameters declared with out, as in Iterable<out Element>.
• contravariant: parameters declared with in, as in ListMutator<in Element>.

If a type parameter in invariant, like the SummableList we have created, then a SummableList<SimplePlayer>, for example, is NOT a subtype of SummableList<Player> (even though it seems logical it should be, because SimplePlayer is a subtype of Player). Because of that, the following code will not compile:

void playGame(SummableList<Player> players) {
    //TODO
}

SummableList<SimplePlayer> players = SummableList { SimplePlayer("Anna") };

// does not compile!
playGame(players);

If a type parameter is covariant, as the type parameter of Iterable, then an Iterable<SimplePlayer>, for example, will be a subtype of Iterable<Player> because SimplePlayer is a subtype of Player, so the above code sample will compile if we substitute SummableList with Iterable:

void playGame({Player*} players) {
    //TODO
}

Iterable<SimplePlayer> players = { SimplePlayer("Anna") };

playGame(players);

Contravariant type parameters can be seen as the opposite of covariant type parameters.

If B is a subtype of A, and there is a type T with a covariant type parameter, then T<B> is a subtype of T<A>, as we’ve seen above.

If T has a contravariant type parameter instead, then T<B> is a supertype of T<A>, not a subtype of it!

Another way of looking at it is to think of a type with a covariant type parameter E as a producer of E, and of a type with a contravariant type parameter E as a consumer of E.

Think about it, you can get instances of E from a non-empty Iterable<E> (by using the property first for example). In a way, you can get Es out of an Iterable<E> (that’s basically why in Ceylon we use the word out to indicate covariance).

Examples of types with contravariant type parameters are usually mutable data structures (we’ll meet them in the next section) which allow adding elements in or just use the elements to provide some service. These types can be seen as consumers of E. We can pass Es in to them, explaining why in is used for contravariant type parameters.

There is a very good discussion of covariant and contravariant type parameters in the Tour of Ceylon, so have a look at it if you want to know more details. For those of you who are interested in the low-level details, this blog post by Gavin King (creator of Ceylon) might be of interest.

Mutability and data structures that can change

Most languages take mutability, or the ability to change values and state, for granted. For example, the following is perfectly valid in Java:

// Java code
String fruit = "apple";
fruit = "orange";
fruit = "banana";

In Ceylon, you wouldn’t normally be able to do that:

String fruit = "apple";
fruit = "orange"; // DOES NOT COMPILE
fruit = "banana"; // DOES NOT COMPILE

Once you’ve assigned the value "apple" to the identifier fruit, you cannot change your mind and say it’s an "orange" or a "banana" instead.

You can also do the following to change the contents of a list (or array, in this case) in most languages:

// Java code
String[] fruits = { "apple", "orange", "banana" };

// change some fruits
fruits[1] = "pear";
fruits[2] = "pineapple";

// comparing two arrays in Java. Enable assertions with the -ea JVM argument
assert(Arrays.equals(fruits, new String[] { "apple", "pear", "pineapple" }));

In Ceylon, you cannot do this using the familiar Iterable and Sequential (you would need to use the Array class, as we’ll see).

Avoiding mutability makes it much easier to reason about the code. You do not need to consider the possibility that any of your values might be modified at any time, almost anywhere in the code base where that data is visible (though scoping alleviates some of this, it cannot solve the problem completely), and that the timing of these changes can be hard to manage, which can potentially cause many bugs.

There are also other considerations that make mutability something you should be careful with, such as visibility across different threads, which we are not yet ready to discuss as we have not met Threads before, that make parallel programming incredibly harder!

Some languages (pure functional languages, notably Haskell) simply do not allow things to be changed at all (but it is still possible to write fully functioning programs in them, though sometimes inconvenient).

Ceylon, on the other hand, does allow changes, or mutability, because there are certain cases which make it quite impractical (or just very inefficient) for the programmer to not be able to change things (we’ll see later how it will be convenient to allow a Pack of cards to change during a game, for example). It is just not the “default” way of doing things because it is understood these days that the cost of unrestricted mutability is too high to compensate for the apparent convenience it provides.

Let’s see how mutability is supported in Ceylon.

For example, if you really want to change the value of your fruit as the program runs, you can annotate fruit with the variable annotation:

An annotation in Ceylon is just a special kind of function that allows extra metadata to be provided and used at runtime to modify the behavior of the program. We have already met some annotations: shared, formal, default, actual, abstract, and now, variable, are all annotations. As usual, this is explained in detail in the Tour.

variable String fruit = "apple";
fruit = "orange"; // OK!
fruit = "banana"; // OK!

Iterables and Sequences are not modifiable (we call them immutable), so you cannot do as in the Java example and change which elements they contain after they’ve been created… but Ceylon does provide mutable (ie. modifiable) data structures such as the simple Array in the language module, and LinkedList, HashMap and HashSet in the ceylon.collection module (more collections will be added in Ceylon 1.1).

Using Arrayin Ceylon:

value fruits = Array { "apple", "orange", "banana" };

// change item at index 1 to "pear"
fruits.set(1, "pear");

// change item at index 2 to "pineapple"
fruits.set(2, "pineapple");

assert(fruits == ["apple", "pear", "pineapple"]);

Arrays are (probably) not used very often in Ceylon because even though you can change them, you cannot add or remove items to make them grow or shrink in size. For that, you can use an LinkedList, for example, from the ceylon.collection module.

To use the collection module, you need to import it in your module.ceylon file:

module hello.ceylonn "1.0.0" {
    import ceylon.collection "1.0.0";
}

Ceylon provides a large number of modules ready to be used out-of-the-box, just enter a new line below the first import in module.ceylon, type import ceylon and hit Ctrl+Space to see what else you can import! The complete list of Ceylon modules, including also third-party modules, can be seen in the Ceylon Herd, which is the Ceylon module repository. Any module from Herd can be imported as shown above: just add the appropriate import in you module file and it will be automatically downloaded.

You are now able to import anything provided by the collection module, such as a LinkedList:

import ceylon.collection { LinkedList }

value fruits = LinkedList { "apple", "orange", "banana" };
fruits.set(1, "pear");
fruits.set(2, "pineapple");

// we can also add some fruit
fruits.add("persimon");
fruits.add("fig");

// ... and remove a fruit
fruits.removeElement("pineapple");

assert(fruits == ["apple", "pear", "persimon", "fig"]);

HashSet is a data structure that can be used to store unique entries efficiently (as in maths, sets cannot contain duplicates). They use the hash code of the items (as we’ve seen before, all Object subtypes have a hash property) they store to make items lookup faster. If you want to avoid having more than one "apple" or "orange" in your fruits collection, for example, just use a HashSet and it will take care of that for you.

As noticed earlier, it is a very good idea to refine the equals and hash methods in each type you expect to store in HashSets or as keys for HashMaps. Also, never store mutable objects in a HashSet or HashMap because if the hash of the object changes after it is added to the container, it will almost certainly become irretrievable!

HashMap can map keys to values and is widely used as a in-memory data storage. We can, for example, use a HashMap to keep the score of each Player in a game:

value player1 = SimplePlayer("Anna");
value player2 = SimplePlayer("John");

value scoreByPlayer = HashMap { player1 -> 10, player2 -> 5 };

value player1Score = scoreByPlayer[player1] else 0;
value player2Score = scoreByPlayer[player2] else 0;

value winner = (player1Score > player2Score) then player1 else player2;

print("``winner.name`` wins!");

The syntax player1 -> 10 creates an instance of Entry<SimplePlayer, Integer>, or, equivalently, SimplePlayer -> Integer. Entries are a convenient way to build maps, as shown above.

Accessing items of the map can be done using square brackets, as shown above, or equivalently, using the get method:

Integer? player1Score = scoreByPlayer.get(player1);

We usually use else defaultValue when trying to access values of Maps because get returns either the value associated with the key, or null if no value exists for that key (notice that values of a Map are restricted to subtypes of Object so you cannot add null as a value in a Map, ensuring that null really represents the absence of a value).

Practice time

In the next section, we will focus less on theory and more on practice, and try to implement a fully functional cards game using all the knowledge we have gained through Parts 1 and 2. You should be able to do it yourself by now anyway, so let me know if you have and I will add a link to your project below!

Stay tuned for Part 3… it’s coming soon!